
Las matemáticas financieras son el campo de las matemáticas aplicadas que analizan, valoran y calculan
materias relacionadas con los mercados financieros, y especialmente, el valor del dinero en el tiempo. Se
ocupan del cálculo del valor, el tipo de interés o rentabilidad de los
distintos productos que existen en los mercados financieros como depósitos,
bonos, préstamos, descuentos de papel, valoración de acciones o cálculos sobre
seguros, entre otras.
Las matemáticas financieras se centran en estudiar el valor del dinero en el tiempo combinando el capital, la tasa
y el tiempo para obtener un rendimiento o interés, a través de
métodos de evaluación que permiten tomar decisiones de inversión. Entre las
herramientas más utilizadas para dichos análisis, encontramos la probabilidad,
la estadística y el cálculo diferencial.
FRACCIONES HOMOGÉNEAS

En el
campo de las matemáticas, una fracción o quebrado es la división de algo en
partes. Si tomamos como ejemplo la fracción ¾ se lee como tres cuartos, y lo
que hace es señalar tres partes sobre cuatro totales. Aquí podemos observar que
lo que da nombre a esta fracción es el número de abajo el cual llamamos
denominador ya que denominamos a la fracción como “tres cuartos”. El número
superior de una fracción, que es el que se divide por el denominador lo
llamamos numerador. Tanto el numerador como el denominador son siempre números
enteros, por lo cual las cifras que representan las fracciones son números
racionales.
LOGARITMO Y PROPIEDADES

Se define logaritmo como el exponente de una potencia con cierta
base, es decir, el número al cual se debe elevar una base dada para obtener un
resultado determinado.
POTENCIACIÓN
En los
hechos, la potenciación es la operación mediante la cual se expresa la multiplicación
de un factor por sí mismo, una cierta cantidad de veces.
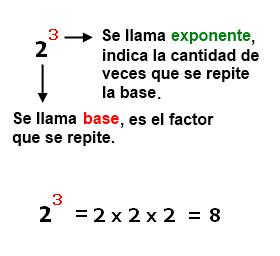
A ese factor se le llama “base” de la potencia y a la cantidad de veces que ha
de multiplicarse por sí mismo, se le llama “exponente” de la potencia.
Ejemplo:
Ejemplo:
PROGRESION GEOMETRICA
Una progresión es geométrica si cada término se obtiene multiplicando
un número constante (razón) por el término anterior.
PROGRESION ARITMETICA
Una progresión es aritmética si cada término se obtiene sumando un
número constante (diferencia) al término anterior.
No hay comentarios.:
Publicar un comentario